What is the capital of Maine?
Credit: Bennian/ShutterstockMaine's capital is Augusta. Have some lobsters, on me!
What is the capital of Montana?
Credit: Sue Smith/ShutterstockHelena is a great place, but don't bother looking for any gold. It's all gone.
What is the capital of Georgia?
Credit: atdr/ShutterstockThe capital of Georgia is Atlanta. While you're there you can check out the World of Coca-Cola!
What is the capital of Nevada?
Credit: Mariusz S. Jurgielewicz/ShutterstockWhile most people go to Nevada for Las Vegas, the capital of the state is Carson City.
What is the capital of Wisconsin?
Credit: Bennian/ShutterstockAny cheesehead knows that Madison is the capital of Wisconsin!
What is the capital of Iowa?
Credit: vepar5/ShutterstockNot West, but just normal Des Moines!
What is the capital of Florida?
Credit: Iantapix/ShutterstockThe correct answer is Tallahassee. Where I'm from, two types of folk: those who ain't, and those who are knee-high on a grasshopper.
What is the capital of Mississippi?
Credit: Mike Flippo/ShutterstockThe correct answer is Jackson, Mississippi.
What is the capital of Oklahoma?
Credit: SNeG17/ShutterstockC'mon! It's right there in the name! The capital of Oklahoma is Oklahoma City.
What is the capital of South Carolina?
Credit: Per Bengtsson/ShutterstockColumbia is the capital of SOUTH Carolina.
What is the capital of Hawaii?
Credit: vepar5/ShutterstockThe right answer is "Honolulu." If you ever visit, participate in a luau just for us.
What is the capital of Michigan?
Credit: Bennian/ShutterstockLansing is the capital of Michigan, home of the Great Lakes.
What is the capital of New Mexico?
Credit: Katherine Welles/ShutterstockSanta Fe is filled with awesome architecture and creative artwork, check it out if you ever go to the capital of New Mexico.
What is the capital of Alabama?
Credit: Kelly vanDellen/ShutterstockNo, it isn't "Bama." Montgomery is the capital, but most people think its Tuscaloosa.
What is the capital of Minnesota?
Credit: Katherine Welles/ShutterstockSaint Paul is the capital of Minnesota, surprisingly not Minneapolis.
What is the capital of Ohio?
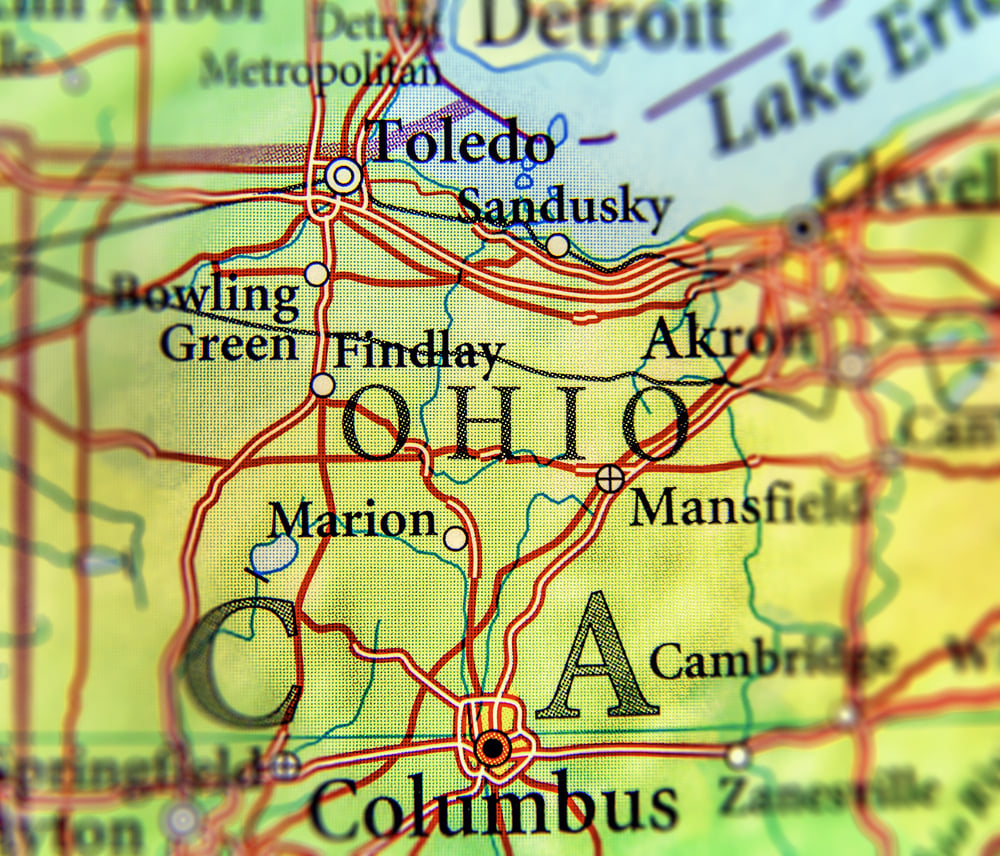Credit: Bennian/ShutterstockColumbus is the capital of Ohio. Cleveland and Cincinnati might be the biggest cities, but Columbus is still the capital.
What is the capital of Kansas?
Credit: vepar5/ShutterstockWe're not in Kansas anymore!... But if you are, check out the capital, Topeka!
What is the capital of Massachusetts?
Credit: vepar5/ShutterstockThe right answer is Boston! I could use some Boston Baked Beans right about now.
What is the capital of Pennsylvania?
Credit: Vladimir Wrange/ShutterstockHarrisburg is not only the capital of Pennsylvania but it's also right next to Hershey, the home of Hershey Park!
What is the capital of Rhode Island?
Credit: Joseph Sohm/ShutterstockProvidence is the capital of Rhode Island, and the state bird of Rhode Island is actually... a chicken!
What is the capital of New York?
Credit: Findelmundo/ShutterstockThe right answer is Albany. Surprise! It's not New York, New York.
What is the capital of New Jersey?
Credit: Paul Hakimata Photography/ShutterstockTrenton is the capital of New Jersey, but you should definitely give Atlantic City a visit if you're in the state.
What is the capital of New Hampshire?
Credit: Jo Ann Snover/ShutterstockConcord is the capital of New Hampshire, they're famous for the White Mountains and mooses!
What is the capital of Texas?
Credit: Leena Robinson/ShutterstockAustin is one of the coolest cities in the country. When you're there, you're probably going to want to check out the live-music scene.
What is the capital of Vermont?
Credit: Magdalena Kucova/ShutterstockMontpelier is the place to go if you have a sweet tooth for maple syrup!
What is the capital of Virginia?
Credit: Mark Time Author/Getty ImagesThe right answer is Richmond, Virginia.
What is the capital of Louisiana?
Credit: Brendan van Son/ShutterstockThe right answer is Baton Rouge. However, if you want to enjoy a trip to Louisiana go to New Orleans instead... trust me.
What is the capital of Washington?
Source: Twitter @WestCoastPicsWhat is the capital of Utah?
Credit: Johnny Adolphson/ShutterstockWhen you're visiting Salt Lake City, be sure to check out the old Olympics venue, it's quite the sight!
What is the capital of Missouri?
Credit: Repina Valeriya/ShutterstockJefferson City is the capital of Missouri, and you can get a great view of the Missouri River from the city.
What is the capital of Idaho?
Credit: Sharon Day/ShutterstockThe capital of Idaho is Boise! If you're there, you have to eat some potatoes.
What is the capital of Illinois?
Credit: Gianfranco Vivi/ShutterstockWhile most people think of Chicago when they hear Illinois, the capital of the state is actually Springfield.
What is the capital of Delaware?
Credit: Joseph Sohm/ShutterstockIf you're ever in Dover, the capital of Delaware, you can brag about being in the first state!
What is the capital of Connecticut
Credit: Millenius/ShutterstockThe right answer is Hartford, the Insurance capital of the USA. That's not really a good thing if you want to avoid people talking at you a lot.
What is the capital of Wyoming?
Credit: LutsenkoLarissa/ShutterstockCheyenne is the capital of Wyoming, and a good drive away north you can visit the Yellowstone National Park.
What is the capital of Kentucky?
Credit: Bhakpong/ShutterstockYou can drown yourself in plenty of bourbon in Frankfort, and check out some fried chicken while you're at the capital of Kentucky!
What is the capital of Colorado?
Credit: photo.ua/ShutterstockThe capital of Denver has arguably the prettiest section of the Rocky Mountains. If you're there, make sure you get some oxygen!
What is the capital of North Carolina?
Credit: Dave Allen Photography/ShutterstockRaleigh, the capital of North Carolina, is famous for their barbecue sandwiches, so you know what you'll be eating.
What is the capital of Nebraska?
Credit: Steve O’Donnell/ShutterstockIf you're in Lincoln, Nebraska, be sure to eat lots and lots of corn!
What is the capital of Maryland?
Credit: Steve O’Donnell/ShutterstockAnnapolis, the capital of Maryland, is both the home of St. Johns College and the United States Naval Academy.
What is the capital of Arkansas?
Credit: Eric Urquhart/ShutterstockOnce you're in Little Rock, Arkansas, you'll realize the rocks aren't so little.
What is the capital of South Dakota?
Credit: visionteller/ShutterstockWhat is the capital of Indiana?
Credit: DaCek/ShutterstockIndianapolis is the capital of Indiana and home to the great Indianapolis 500!
What is the capital of Arizona?
Credit: Alena Vezza/ShutterstockTry not to collapse from dehydration in the desert when you're in the capital of Arizona... Phoenix!
What is the capital of North Dakota?
Credit: Zack Frank/ShuterstockWhat is the capital of California?
Credit: Frederic J. Brown/AFP/Getty ImagesThere are some huge cities in California, but surprisingly the capital is Sacramento.
What is the capital of West Virginia?
Source: Rhonda Humphreys/Wikimedia Commons; https://creativecommons.org/licenses/by-sa/4.0/deed.enVirginia City
What is the capital of Oregon?
Source: wikipedia commonsSalem is the capital of Oregon, but there's also one in Massachusetts. Don't get them confused!
What is the capital of Alaska?
Credit: Ditty_about_summer/ShutterstockWhat is the capital of Tennessee?
Credit: highspeedinternet.com/safewiseYou've got a 3 in 4 chance if you guessed a "ville." If you're ever in Tennesee, we'd recommend checking out Dollywood!
